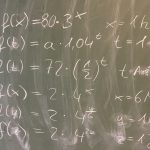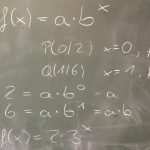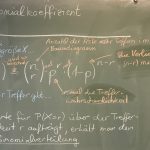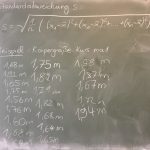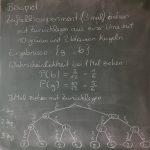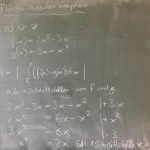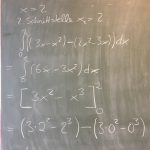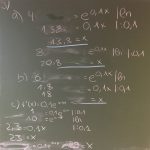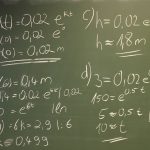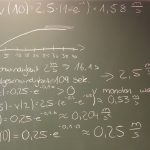Kurs Q1 Mathe

Schöne Ferien!

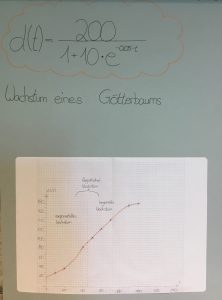
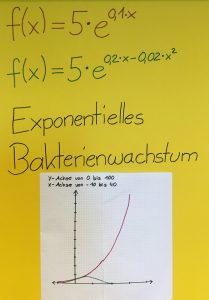
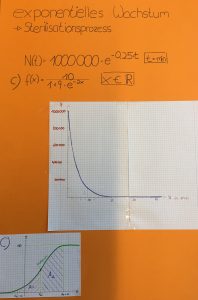
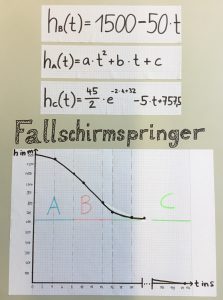
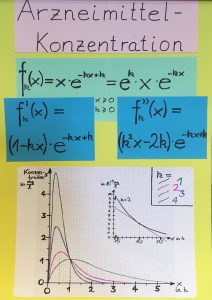
2018-06 Übungsaufgaben zu Wachstum (exponentiell/ begrenzt/ logistisch) und zur e-Funktion

2018-05-17 Uff, war das anstrengend. Aber manchmal schafft die Schwarmintelligenz leider nur alternative Fakten. So ist es richtig (und so war es richtig, als es das erste Mal an der Tafel stand )

Zu Aufgabe 1d: wenn y= 1 Monat ist, muss 4^1 bei y=6 herauskommen, also f(y)=2 * 4^(y/6), analog für z= 1 Jahr

Zu Aufgabe 2: In der Funktion für den Abbau muss die neue abgebaute Menge immer zur alten addiert werden. Das ist explizit schwierig zu formulieren, rekursiv siehe Bild für 1-3h. Einfacher ist dann f(t)= 50 – 50 * 0,7^t = 50 * (1-0,7^t)

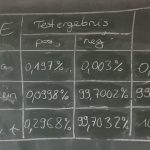
2018-05-08 Sigma-Regeln, Vertrauensintervalle, Abschluss Stochastik

2018-05-03 Klausur Stochastik

2018-04-26 Wdh. und Übungsaufgaben für die Klausur, Abituraufgaben aus Vorjahren

2018-04-24 Binomialverteilte Zufallsgrößen: Bestimmung von n und p; Sigma-Umgebungen

2018-04-19 Binomialverteilte Zufallsgrößen: Erwartungswert und Standardabweichung

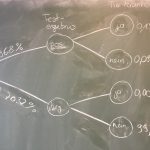
2018-04-17 Übungen zur Berechnung von kumulierten Wahrscheinlichkeiten, binomcdf

2018-04-12

2018-04-10

2018-04-05

2018-03-15

2018-03-13 misslungener Versuch, Reaktionszeiten mit einer excel-Datei zu messen und auszuwerten

2018-03-08

Auswertung: Mittelwert 1,68m, n=21, Standardabweichung s ≈10, Median (mittlerer Wert) 1,68m, Modalwert (am häufigsten vorkommender Wert) 1,68m

2018-03-06

2018-03-01

2018-02-27

2018-02-22

2018-02-20 Wahrscheinlichkeit: Wiederholung der Begriffe, Regeln und Darstellungsarten statistischer und stochastischer Experimente

2018-02-15 Klausur P4 Integrale

2018-02-13

2018-02-08 Integral und Flächeninhalt:

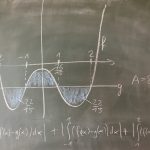
zw. Graph und x-Achse: Nullstellen ermitteln, Teilflächen berechnen (Beträge der Integrale), addieren, zack – fertig.

zw. 2 Graphen: Schnittpunkte ermitteln, Differenz der Funktionen bilden, Betrag des Integrals der Differenzfunktion entspricht der Fläche zwischen den Graphen, zack – fertig.

2018-02-06 Gemeinsames Erstellen einer möglichen Klausur zum Thema Integrale.

2018-01-30 Übungen Flächeninhalte zwischen Graphen bestimmen, Sachaufgaben.

2018-01-25 Flächeninhalte zwischen Graph und x-Achse sowie zwischen zwei Graphen.

2018-01-23 Bestimmung von Stammfunktionen. Lineare Substitution (Kettenregel rückwärts)

2018-01-18 Bestimmung von Stammfunktionen. Potenzfunktionen, Summenregel, Produktregel

2018-01-16 Haupsatz der Differential- und Integralrechnung

2018-01-11

2018-01-09

2017-12-19 Gruß von der Klasse 3a:

2017-12-14 Funktionenscharen – Anwendungsaufgaben S. 96 Nr. 8 und 9

2017-12-12 Funktionenscharen, Ableitungen mit Parameter (S. 95, Nr. 1,2,3)

2017-12-07 Anwendungsaufgaben zu exponentiellem Wachstum

2017-12-05 Umkehrfunktionen, natürlicher Logarithmus

2017-11-30 Die Exponentialfunktion [latex size=0 color=000000 background=efefef]\displaystyle f(x)=e^x[/latex] ist die Funktion, bei der jeder Funktionswert gleich der Tangentensteigung ist. Für die Exponentialfunktion gibt es also eine neue Ableitungsregel: [latex size=0 color=000000 background=efefef]\displaystyle f(x)=e^x\Rightarrow f'(x)=e^x[/latex]. e ist dabei die „Eulersche Zahl“, eine nicht abbrechende, nicht periodische Zahl. Sie hat gerundet den Wert 2,7

2017-11-28 Produktregel: Bei Produkten von Funktionen f(x) = u(x) * v(x) lautet die Ableitungsfunktion f'(x) = u'(x)*v(x) + u(x)*v'(x).

Umgehung der Quotientenregel: Wenn ein Term mit x im Nenner steht, setze Klammern darum und schreibe das ganze als Produkt, dann Produktregel benutzen.

2017-11-23 Kettenregel: Bei verketteten Funktionen f(x) = u(v(x)) lautet die Ableitungsfunktion f'(x) = u'(v(x)) * v'(x) oder umgangssprachlich: äußere Ableitung mal innere Ableitung.

2017-11-21 Verkettete Funktionen – Was ist das? Beispiele S. 80 Nr. 4 und Nr. 6

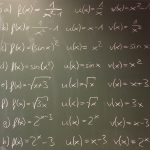
2017-11-14 Vermischte Übungen und Fragen zur Klausur. Was drankommt? Alles, was hier unterhalb steht.

2017-11-09 Vermischte Aufgaben zur Trassierung. Linke Funktion und rechte Funktion mit jeweiliger Anschluss-Bedingung werden ausgewürfelt.

Operatoren („Tu-Wörter“ :-)) für Klausuren im Fach Mathematik: Operatoren_Mathematik

Darstellung stückweise definierter Funktionen mit dem GTR:

Addition der Teilfunktionen, werden durch Angabe der Bedingung hinter dem jeweiligen Funktionsterm eingegeben. Zur besseren Übersicht kann man zunächst die einzelnen Funktionen eingeben und danach addieren:

[latex size=0 color=000000 background=efefef]\begin{array}{ccl}Y_1&=&2\\Y_2&=&2X+4\\Y_3&=&-X+10\\Y_4&=&Y_1\{X\le-1\}+Y_2\{X>-1\}\{X<2\}+Y_3\{X\ge2\}\end{array}[/latex] ergibt für Y4 den Graphen

2017-11-07 Trassierung: glattes Verbinden von zwei vorgegebenen Funktionen, zwischen denen ein Stück fehlt (Bsp.: Straßenbau nach Grenzöffnung)

Trassierung

Bedingungen für die Anschluss-Stellen notieren, n Stück
Werte g(x) (stetig), g'(x) (diffbar), g“(x) (ruckfrei) berechnen
Trassierungsfunktion: Polynom (n-1)-ten Grades für f allgemein ansetzen
Anschluss-Stellen Als x in f (stetig), f ‚ (diffbar), f “ (ruckfrei) einsetzen
LGS mit n Gleichungen für n Koeffizienten aufstellen, führt auf n x (n+1) – Matrix
weiter wie unten

Bestimmung von Funktionstermen aus Eigenschaften

Allgemeinen Funktionsterm aufschreiben; i.d.R. ein Polynom [latex size=0 color=000000 background=efefef]\displaystyle f({x})=ax^{n}+bx^{n-1}+cx^{n-2}+\dots[/latex]
Bedingungen einzeln aus der Aufgabe ermitteln und mathematisch notieren ( f(x)-Schreibweise )
Symmetrien auswerten: Achsensymmetrie -> nur gerade Exponenten von x; Punktsymmetrie zu O -> nur ungerade Exponenten von x. Die anderen Koeffizienten sind dann Null.
Du brauchst so viele Bedingungen, wie es (übrige) Koeffizienten gibt.
LGS aufstellen -> pro Bedingung eine Gleichung
LGS per Hand lösen oder Matrix notieren („erweiterte Koeffizientenmatrix“)
Matrix „diagonalisieren“ mit rref([A])
Ergebnis: Funktionsterm mit den ermittelten Koeffizienten notieren.

2017-11-02 Übungen zur Bestimmung von Funktionstermen aus Eigenschaften. S. 64/65 Nr. 2, 9, 12, Ansatz 13.

HA: 13 beenden und Lösung überprüfen:

2017-10-26 LGS mit Parametern (S. 59 Nr. 11/12) und mit besonderen Lösungsmengen (S. 61/62) lösen. Funktionsterme aus Punkten bestimmen S. 64 Nr. 1

2017-10-24 LGS lösen mit dem GTR. Umgang mit Matrizen. Befehle ref([A]) und rref([A])

2017-10-19 Schreibweise von LGS als erweiterte Koeffizientenmatrix:

Schematische Betrachtung Gauß- und Gauß-Jordan-Algorithmus:

Gauß führt im „Normalfall“ (eine Lösung des LGS) zu Dreiecksform, Gauß-Jordan zu Diagonalform (erweiterte Einheitsmatrix).

„Spezialfälle“:

letzte Zeile 0 0 0 1 ⇒ keine Lösung;
letzte Zeile 0 0 0 0 ⇒ ∞ viele Lösungen, zu ermitteln aus vorletzter Zeile der Matrix und dann rückwärts einsetzen.

Lösen von LGS mit dem TI-84 mit Hilfe von Matrizen und den Befehlen ref() (Gauß) oder rref() (Gauß-Jordan) Infoblatt LGS mit dem TI-84

2017-10-17 Kleiner Einschub eines Algebra-Themas, das wir als Werkzeug für die folgenden Problemstellungen benötigen: Gauß-Verfahren zum Lösen linearer Gleichungssysteme (LGS).

2017-09-28 Aufgaben Rückblick auf gesamtes Thema S. 52/53. Zum Erhalt der grauen Mathezellen im Gehirn gerne von diesen Seiten in den Ferien mehr bearbeiten, vielleicht sogar in Arbeitsgruppen so wie heute. Und: Zur Wiederholung Gleichungen lösen und Terme umformen. Das hilft. Schöne Ferien.

2017-09-26 HA besprochen, Wiederholen – Vertiefen – Vernetzen S. 46 Nr. 6 gemeinsam gelöst. Vorbereitung auf Do: S. 52/53 durch gedachtes Koordinatenkreuz vierteilen, aus jedem Quadranten eine Lieblingsaufgabe aussuchen, die dann am Do gerechnet wird.

2017-09-21 Extremwertprobleme S. 41 Nr. 5-11. Lösungen Nr. 5, 6, 7, 9: Ergebnisse der Gruppenarbeiten, korrigiert Lösungen zu Nr. 10 & 11 sind im Buch.

HA zu Dienstag: Nr. 8 daran kann man nochmal üben, mit Brüchen und Gleichungen umzugehen. Lösung zur Kontrolle

2017-09-19 S. 38 Nr. 10 Anwendung – Sachzusammenhang. Besonderheit: finden des richtigen Windows für die sinnvolle Darstellung im GTR. Tipp: x-Wert festsetzen (hier z.B. 80), y-Wert dazu berechnen (GTR: Y1(80) enter oder in Table suchen), window einstellen. Auch die Achseneinteilung sinnvoll anpassen!

Extremwertprobleme mit Nebenbedingungen: Darstellung einer Variable durch eine andere mit Hilfe der Nebenbedingung, man erhält durch Einsetzen eine Funktion, die nur noch von einer Variablen abhängt. Von dieser Funktion kann man mit analytischen Methoden oder mit dem GTR Maximum oder Minimum bestimmen. Dazu S. 40 Nr. 3&4, es ergibt sich jeweil ein Quadrat als extremale Figur.

2017-09-14 S. 34 Nr. 10 mit GTR gelöst, Funktion in Y1; Ableitung in Y2 eingeben: math->8:nDeriv d/dx (Y1)|X=X , dann braucht man die Funktion nicht selbst abzuleiten. (2. Ableitung ginge dann mit math->8:nDeriv d/dx (Y2)|X=X in Y3)

Fachbegriffe in Sachzusammenhängen: S. 36 Nr. 1 und 2, gelöst mit GTR. Übungsmöglichkeit für zu Hause: Nr. 2 per Hand nachrechnen -> Wiederholung Kurvendiskussion

2017-09-12 Aufgaben S. 33, Nr 6a; S. 34 Nr 9 Lsg: P(-2/2) & 10 angefangen

2017-09-07 Aufgaben S. 33, Nr 1: Gleichungen erstellen. Lösungen:

a) t: y gleich vier x minus vier; n: y gleich minus ein Viertel x plus vier komma fünf
b) t: y gleich minus ein Achtel x plus eins; n: y gleich 8 x minus einunddreißig komma fünf
c) t: y gleich x; n: y gleich minus x

Nr. 2: tangierten Punkt finden. Es gibt immer zwei Lösungen der quadratischen Gleichung y = ux – ½ u² (hier die Tangentengleichung)

a) P1(0/0) und P2(2/2); Tangenten: y = 0 und y = 2x – 2
b) Q1(0/0) und Q2(-2/2); Tangenten: y = 0 und y = – 2x – 2
c) R1(2/2) und R2(-2/2); Tangenten y = 2x – 2 und y = – 2x – 2
d) S1(5/12,5) und S2(1/0,5); Tangenten y = 5x – 12,5 und y = x – 0,5

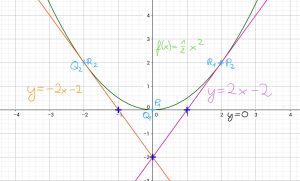
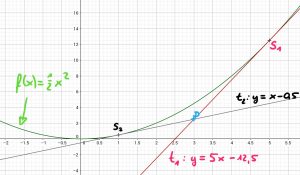
Zum weiteren Üben eignen sich S 34, Nr 5 und 6, Lösungen sind hinten im Buch.

2017-09-05 Tangenten- und Normalengleichung S. 32

2017-08-31 Tangenten an Graphen S. 31 Nr. 11 und 14a) Expertenaufgaben können abgegeben oder vorgetragen werden, bei Vortrag bitte bis Mo bei mir melden.

2017-08-29 Notwendige und hinreichende Bedingungen; Polynomdivision (siehe auch: Wikipedia oder DorFuchs); nützliche Apps: Math 42; GeoGebra; PhotoMath; GTR Anleitung TI-84; GTR Tipps

2017-08-24 Kurvendiskussion am Beispiel f(x) = (x+2)(x+5)(x-2)(x-1) Infoblatt: Kurvendiskussion

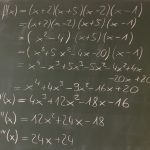
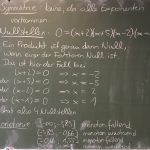
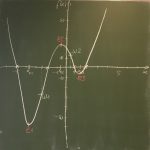
2017-08-22 Kurvendiskussion am Beispiel f(x) = ²/3 x³ – 18 x Arbeitsblatt: Kurvendiskussion leer

2017-08-17 HA: Anwendung der Ableitungsregeln; S.19, Nr.4 Berechnung von Punkten mit gegebener Steigung „per Hand“, dabei Wiederholung der p-q-Formel zum Lösen quadratischer Gleichungen.

HA zu Do: S. 19, Nr. 2 (Wand: a,d; Mitte b,e; Fenster c,f) Terme zunächst eventuell umformen!

2017-08-15 Wiederholung Ableitungsregeln Potenz-, Summen-, Faktor-Regel S. 18.

2017-08-10 Aufgaben zum Grundverständnis der Funktions-Schreibweise S. 16/17 Nr. 1, 2, 3, 5, 6, 7, 10

2017-08-08 Arbeitsblatt: Begriffe und Zeichen, Begriffswiederholung zum Thema Ableitung

2017-08-03